Membrane Potentials
Learning Objectives
1. Know how ion diffusion in ion channels establishes membrane potentials
When an ion-selective ion channel opens in the membrane, specific ions can move down their electrochemical gradient (this gradient is a combination of electrical and concentration gradients). By moving charges from one side to the other, the resulting ion currents change the total charge in the cell and the electrical potential across the membrane. Without charge movement, there can be no membrane potential change
2. Recognize that fluxes needed to make typical membrane potentials are extremely small: membrane capacitance
Membrane capacitance is by definition the amount of charge you have to move across the membrane to change the membrane potential a certain amount. In cells, the membrane capacitance is small, so the quantity of ions that has to move for electrical signaling is tiny, depleting the existing gradient by only a little.
3. Explain with Na+, K+, Cl–, and Ca2+ what contribution each could make individually to electrical potential changes in the plasma membrane of excitable cells.
Na+, K+, Cl– and Ca2+ ions have different ion gradients and charge. Therefore, opening selective ion channels for each of them pulls the membrane potential towards a different final value. For example, open K+ channels produce a negative inside potential, and open Na+ channels produce a positive inside potential. Therefore electrical responses of cells depend on opening the right ion channels in the right sequence to shape the signal.
Standard laws of electricity govern how cells make electrical signals across their membranes. This chapter reviews these laws. The need to think about electricity may seem daunting to some biologists, but really it is not particularly complicated. Electricity obeys a few simple physical rules in a logical manner. You have studied them before. Comfort with the key concepts in this chapter will be very helpful in subsequent more specific and detailed study of electrophysiology. As we will see, if you have both (i) gradients of ions across a membrane and (ii) a membrane permeability to some of these ions by open ion channels, the necessary net flow of the charged ions in these channels forms an electric current and can change the membrane potential.
To motivate our study of principles, we look ahead at a nerve cell sending an electrical message, the spike-like action potential (we will examine this process in more detail later in the course). The action potential is a stereotyped, efficient, brief, electrical signal that can travel regeneratively at high speed along an axon. It is the long-distance, electrical message of the nervous system, the unit of information like the information bits in the wires of a computer. Figure 1 is an electrical recording from the inside of an active nerve cell. We will note just three typical properties for now. (i) This neuron starts with a NEGATIVE inside resting potential (-60 mV). (ii) During the action potential, the inside of the cell becomes briefly POSITIVE. And (iii) the whole signal is finished in <1 ms (0.001 s). Think of this signal as a brief membrane potential excursion of about 100 mV, the pulse-like unit of propagated information. We will begin to explain in physical terms how cells make electrical signals like this and how they propagate.
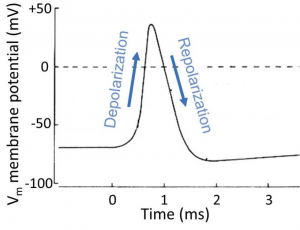
Important convention. Note that when we speak of membrane potentials of the plasma membrane, we consider the inside potential relative to the outside. In simple terms you can think of this as the potential INSIDE the cell. The whole potential drop occurs in a region of <10 nm as you cross through the insulating membrane.
Learning objective 1. Describe elements of ionic electricity: ions, charge, potential gradients, forces, current, conductance, and membrane capacitance
An Analogy: If it is helpful, you can make an analogy between familiar gravitational rules and less familiar electrical rules. The mass of an object is analogous to electrical charge. The gravitational potential is analogous to electrical potential (voltage). You have to do work to lift a mass to higher gravitational potential, and similarly you have to do work to move a charge to a region of higher electrical potential. One real difference is that charges, voltages, and forces can be either positive or negative, attractive or repulsive, but masses, gravitational potential energy, and gravity are always positive and attractive.
First rules of ionic electricity. These rules are important to understand physiology. They are also summarized in a separate one-page file “Electric Keywords” that we hope you will keep referring to as you study electrophysiology. Please make sure that you are comfortable with them!
- Charge: Ions have a charge given in multiples of one elementary electron charge. Cations (Na+, K+, Ca2+) are positively charged and anions (Cl–) are negatively charged.
- Two forces that move ions: (i) Charges are moved by the force of electric fields: Opposites attract, so cations (positively charged) move towards a negative pole, and anions towards a positive pole. (ii) In addition, ions are moved by diffusion (thermal agitation) down their concentration gradients–even in the absence of electric fields.
- Current: A net movement of charge (flow of ions) is an electric current (an ion current) measured in amperes (A) and symbolized by I. The direction of current is defined by convention as the direction of positive charge movement. Hence, if only positive K+ ions are moving OUT of a cell, then electric current is also moving OUT of the cell; however, if only negative Cl– ions are moving OUT of the cell, we use this convention to say that electric current is flowing INTO the cell.
- Voltage: If cations are removed from a compartment (the cell), the compartment becomes more negative, i.e, a negative electrical potential or negative voltage will be set up inside the cell. The voltage arises because there is a charge imbalance. In electrophysiology, the words voltage and electrical potential will mean the same thing. A voltage is measured in units of volts (V) and symbolized by V. It is defined as the amount of electrical work it would take to remove one more cation. [Aside: When you buy a flashlight battery, it is typically a 1.5 volt battery. We could write Vbattery = 1.5 V. The bigger the battery (AAA,AA,A,B,C,D, etc.), the more current and charge it can provide, but the alkaline battery chemistry always makes a 1.5 V potential. In biology, the membrane potentials are much smaller, within the range from -100 mV to +50 mV. All our electrical signaling occurs within this small voltage range as in Figure 1.]
- Conductance: Conductance is a measure of how easily ions can cross the membrane (it is the inverse of the resistance). A membrane with many open ion channels has a high conductance (low resistance), and one with no open ion channels has a conductance that is almost too low to measure since the lipid bilayer is very impermeable to charged ions. Thus conductance, symbolized G, is proportional to the number of ion channels open. We now show how to measure it.
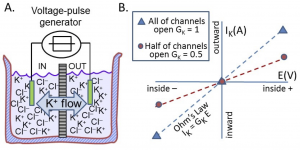
An electrical experiment to measure conductance of a membrane (Figure 2A): A beaker with electrolyte solutions is divided into two compartments called IN and OUT by a membrane containing only K+ channels. The IN and OUT compartments contain equal concentrations of dissolved KCl and each has an immersed electrode (e.g. a wire, green) connected to a voltage-pulse generator. The pulse generator changes the potential on the wire for brief periods and can make the IN side briefly negative, positive, or unchanged. Figure 2B plots the results as blue triangles. These triangles show the measured current IK carried by K+ ions versus the applied voltage. (i) When the transmembrane voltage is kept at 0 mV, no net K+ current flows (symbols at the origin). There is no force on the K+ ions. (ii) When the IN voltage is made negative, there is an inward K+ current, the negative electrical potential pulls K+ ions towards the IN compartment. (iii) when the IN voltage is made positive, there is outward K+ current.
The blue triangles in Figure 2B describe a straight line through the origin. The conductance is the slope of this line. This illustrates Ohm’s law
IK = GK E
which says that K+ current IK is linearly proportional to GK (the conductance to K+) and the electrical driving force E. Remember that the conductance is the inverse of the resistance (G = 1/R), which connects the equation above to the more familiar form of Ohm’s law (E = I R). Ohm’s law tells us that more force (more E) means more current.
The blue line and blue symbols in Figure 2B describe the current when all the K+ channels are open. If we close half of them, we get the red line. As you might expect, the flow of K+ is reduced to half, the slope is only half, and the conductance of the membrane is half. Electrical conductance is easy for electrophysiologists to measure and conveniently tells us how many ion channels are open. This concept is used repeatedly when we start with electrophysiology.
Learning objective 2. Know how ion diffusion in ion channels establishes membrane potentials
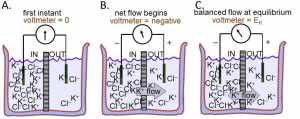
A thought experiment on membrane potentials: We now use these rules of electricity to describe the origin of membrane potentials (Figure 3). Again electrolyte in a beaker is divided by a membrane containing only K+ channels. But now there is no pulse generator, just a recording amplifier that reports any potential difference that might appear spontaneously across the membrane. These compartments, for example, could represent the inside and the outside of a cell with a K+-permeable membrane since this time, more like a real cell, the IN compartment contains high K+, and the OUT compartment, low K+ (Figure 3A). Each solution is initially electrically neutral with an equal number of anions and cations, and the voltmeter cartoon indicates that there is initially no potential difference between them. Rule 2 and your intuition say that K+ ions will start to flow towards the OUT compartment because they are free to diffuse down their concentration gradient (Fig. 3B). Since there are no Cl– channels in the membrane, there is no movement of Cl– ions across this membrane. Thus, there is a net movement only of positive charges, and Rule 3 says that the outward K+ flow carries an outward electric current IK. Rule 4 says that since positive charge is being removed from the IN compartment, that compartment starts to become more negative–as indicated by the second voltmeter cartoon. A membrane potential has been generated!
However, rule 2 says that the net flow of K+ cations will soon slow down as they experience an electrical retarding force from the growing membrane potential that makes it progressively harder for them to leave the negative IN compartment. An equilibrium is reached as the opposing electrical force pulling K+ ions back becomes equal to the diffusion force pushing them out (Fig. 3C). The forces have become balanced. Now the membrane has established a stable negative internal membrane potential all by itself! This whole process takes only a millisecond or two. The potential difference arose because (i) there is a K+ gradient, and (ii) the membrane has K+-selective ion channels. This thought experiment corresponds very closely to the situation in real cells. They have K+ inside and they have a negative resting potential inside (Fig. 1) because of a predominance of open K+ channels at rest. We have applied Rule 4 to understand the negative resting potential and now generalize with the most important concept to understand electrical signaling:
Take–home concept 1. To create or change the cell membrane potential requires a net movement of charge (ions) across the membrane. This concept means that the action potential of Fig. 1 must be produced by net movements of ions (charge) across the membrane.
Learning objective 3. Recognize that fluxes needed to make typical membrane potentials are extremely small
Our last rule of electricity says that very few ions need to move to produce sizable changes in membrane potential:
6. Capacitance: Electrical capacitors store charge. Recall that a substance like the lipid bilayer that does not conduct electricity is called an insulator. Two conductors separated by a thin insulator form an electrical capacitor. Therefore, the thin plasma membrane bathed by inside and outside conducting electrolyte solutions has the property of an electrical capacitor. The magnitude of a capacitance (symbolized C) is defined as the number of charges that you have to put on the capacitor to achieve a certain potential change. Therefore, the capacitance of cell membranes tells us how many ions have to be moved across the membrane to change the membrane potential during signaling. For a spherical neuron 20 m in diameter, a net movement of only ~10-17 moles of cations into the cell will be enough to make the inside 100 mV more positive–equivalent to one action potential. This movement amounts to only 0.002% of the number of cations already in the cell (~6×10-13 moles). Therefore, the ion fluxes needed to make signals in biological membranes are tiny, and the charge movement and potential changes can be completed quickly. However, after repeated bouts of signaling it becomes essential to accelerate ion pumps to restore the gradually declining ion gradients. This need for accelerated pumping is accentuated in fine nerve processes where a large surface-to-volume ratio means that the reserve pool of ions inside is smaller.
Take–home concept 2: Although the membrane capacitance does require that some ions move to generate electrical signals (concept 1), the quantity can be quite small so that a single action potential does not disturb the existing ion gradients very much.
Learning objective 4. Explain with Na+, K+, Cl– and Ca2+ what contribution each could make individually to potential changes in the plasma membrane of excitable cells.
The three questions approach: We begin with three questions that will allow us to determine what each ion can do to the membrane potential. We have just applied these questions to the K+ ion in Figure 3. Now we generalize. No equations, just simple logic that goes a long way.
Question 1: Which ion is permeable?
Question 2: Which direction does it want to flow?
Question 3: What membrane potential would that induce?
For Figure 3, the three answers were:
- K+ is permeable;
- It would flow OUT;
- That would make the voltage of the IN side negative.
Now you can go through each of the ions in Table 1, supposing that the membrane is selectively permeable only to K+, Na+, Ca2+, or Cl– one at a time, using the three questions to decide what sign of membrane potential would result. You should have found two ions that could make the membrane potential negative and two that could make it positive. Excitable cells open and close ion channels to each of these ions to generate their electrical signals. In particular, you will learn shortly that for the nerve cell in Figure 1, the resting membrane is K+ permeable and therefore negative inside; the membrane during the action potential becomes Na+ permeable (Na+ channels open) and therefore a few Na+ ions move in and the potential becomes positive; and then the Na+ channels close, and K+ channels bring the membrane back to the negative resting potential.
Recap: Let us apply our learning to the action potential (AP) rising phase in anticipation of your next session on electrical excitability. The AP rising phase requires net entry of Na+ ions (Rule 3). The number of ions moving is modest (Rule 6). Nevertheless, repetitive firing of APs will lead to intracellular Na+ accumulation, so, since its Na+ substrate increases, the Na+/K+-ATPase pump speeds up and pumps the Na+ out again more vigorously. Local glucose metabolism speeds up a bit to make the needed ATP. A brain imaging technique called PET scan measures glucose consumption and allows radiologists to observe which brain regions become active during specific mental activities. Soon, you will also learn that our larger nerve fibers often use myelin as a way to reduce the electrical capacitance of sections of axon. In myelinated nerve, Schwann cell membranes are wrapped on top of each other in many tight layers around the axon, reducing the effective capacitance and reducing the amount of ion movement needed to make an action potential. This permits faster depolarizations with smaller Na+ flow (Rule 6) and faster propagation of the action potential message. We will return to this later.
The Nernst Equation: So far we have been thinking qualitatively about the sign of the membrane potential, and that suffices for basic understanding. However, sometimes we want to say how large the membrane potential will be rather than just working out its sign. Scientists need to do this to check that they really understand what is going on. For this, we return to the thought experiment of Figure 3. In the right panel, the membrane potential comes to an equilibrium value where the concentration force pushing K+ ions out of the IN compartment is exactly matched by the electrical force pulling them back. This is an electrochemical equilibrium and therefore thermodynamics can give us an expression for the equilibrium potential. Since the problem involves a membrane selectively permeable only to K+ ions, we call this the “potassium equilibrium potential” symbolized by EK. For completeness we write the answer called the Nernst Equation first in its general thermodynamic form for any ion with charge z, but then follow by writing a much more practical version for our body temperature in millivolts. If you do need to calculate equilibrium potentials, use the practical form. You should understand the significance of the Nernst Equation as a beautiful and compact explanation, but in general practice, you would rarely have to use it.
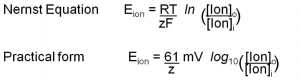
In the formal first form, there are thermodynamic constants: R (gas constant), T (temperature), and F (Faraday’s number). In the practical form, their values have already been factored in for 37ºC. Notice that the equilibrium potential depends on the ratio of the ion concentration outside and inside. The ratio appears inside a logarithm. Box C reminds us that log10 (x) equals the power of 10 that would give the value x. It is also a button on your calculator!

Conceptual Significance of the Nernst Equation. With the practical form of the Nernst equation, we can plug in the ion concentrations listed in the chapter on Cell Membranes and Transporters to get the equilibrium potentials of each of the four important ions (Table 1). These values define the range of plasma membrane potentials that cells are able to achieve. As expected from the three-questions approach, EK is a negative number, -97 mV. That is as far negative as the plasma membrane potential ever gets. To do so, the membrane would have to be exclusively permeable to K+ ions; that is, the only ion channels open would be K+ channels. In resting axons, open K+ channels greatly outnumber open Na+, Cl–, and Ca2+ channels so the plasma membrane is primarily permeable to K+, and the resting potential approaches EK. By contrast, but as expected from the three-question approach, ENa is a positive number, +65 mV. As you will see shortly, ENa sets the positive limit of the nerve action potential (Figure 1) when mostly Na+ channels are open. Remember that at the equilibrium potential for an ion, the diffusion force and the electrical force are exactly balanced (they cancel each other) and there would be no further net flow of that ion. In several disease or nutritional conditions the ion gradients across our cell membranes change. This can severely impact the resting potential and the electrical signaling of nerve and muscle.
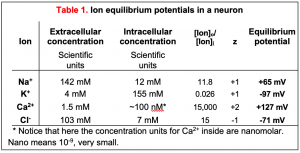
Key concept: Real membranes have several types of open channels. Although we say the resting potential is negative because K+ channels are open there, the resting potential is never as negative as the ideal EK (-97 mV). This is because even at rest, there are some open Na+ and Cl– channels whose equilibrium potentials are more positive than EK (+65 and -71 mV in Table 1 for neurons). When several different channels are open simultaneously, the membrane potential (Vm) will lie somewhere between the equilibrium potentials of each of those channels. Thus, if the conductance to K+ is the largest at rest, Vm will be brought closer to EK, and if the conductance to Na+ rises, Vm will depolarize, eventually approaching ENa if the Na+ conductance becomes the largest. This important concept will explain how excitable cells make electrical signals (membrane potential changes) in the nervous system by opening and closing ion-selective channels.
REVIEW QUESTIONS
The membrane potential is symbolized by VM in these review questions.
PRACTICE QUESTIONS
