5 Monte Carlo Simulation in Construction

Introduction

Risk and uncertainty are baked into every aspect of a construction project, whether stemming from fluctuating material costs, unpredictable labor markets, permitting delays, or site conditions. Despite this, the industry often relies on deterministic forecasting models that fail to reflect the full range of possible outcomes. Monte Carlo Simulation (MCS), a stochastic method developed during the mid-20th century, allows for the modeling of uncertainty through thousands of simulations across varying input scenarios. This technique can provide more realistic, risk-adjusted projections of cost and schedule, which can ultimately reduce delays and improve efficiency.

Motivation

I will begin by stating that Monte Carlo Simulation is a core component of my master’s thesis, where I explore its application to opportunistic real estate development projects from an architectural perspective. Accordingly, this paper will serve as a first pass to ground myself in the broader history and practical nuances of MCS and its use in the design of the built environment. Early stages of my research suggest that while MCS is virtually absent from architectural practice, it sees limited but growing application within construction management and real estate. Still, its use remains far below the level it could or arguably should reach, especially when compared to engineering and science disciplines outside of Architecture/engineering/construction (AEC).

Purpose & Research Question

The purpose of this project is to examine how MCS has been used within the construction industry and to evaluate both its strengths and its limitations. This includes identifying the core benefits it provides (clearer risk visualization, contingency planning, and decision making to name a few) as well as the practical and institutional gaps that prevent its widespread use. The broader goal is to contribute to a more nuanced understanding of MCS’s current role in construction and to explore how education, policy, or practice might evolve to support more innovative and routine use of probabilistic tools.

What explains the persistent gap between MCS’s demonstrated value and its limited adoption in construction practice? This study investigates how MCS is currently used, what barriers prevent its wider integration, and where opportunities lie for it to reshape risk assessment and decision making in architecture and construction. Ultimately, it challenges the industry to reconsider how it confronts uncertainty, and whether tradition is an obstacle or a foundation for innovation.

Methods

The project will draw from a variety of sources. A literature review and case study will attempt to cover peer-reviewed articles focused on several use cases of MCS in construction, highlight both successful and limited applications of the method. Additionally, an interview with a faculty member from the University of Washington’s Construction Management department will offer insight into how MCS is currently taught, perceived, and used by Construction Management professionals and students alike. Finally an example MCS is developed to visualize and demonstrate its capabilities and address if an argument towards industry implementation holds water.

What Exactly is MCS?

Its name derives from the casino in Monaco, a nod to the chance driven world of gambling. While its name is a punny nod to the roll of the dice, Monte Carlo Simulation quickly learned to deal with much hotter chips. MCS has a nuclear past, as it was developed during the Manhattan Project in the 1940s to model probabilistic systems far too complex for deterministic math alone (Metropolis & Ulam, 1949). MCS is the culmination of wartime urgency and the understanding that not all systems can or should be predicted with certainty. As computing power grew, so did the sophistication of simulation. By the 1960s, researchers had developed the methods that ultimately gave rise to evolutionary computing. Quantum Monte Carlo techniques also emerged with early insights from Enrico Fermi and other notable scientific minds. Over the decades, MCS has become a staple in fields where uncertainty is not just present, but defining, like nuclear physics, quantitative finance, medical research, et al. Outside of the hard STEM fields, MCS has been utilized in art and design, law, and emergency response operations. What began as a wartime necessity has since matured into a broad, powerful toolkit for modeling uncertainty across disciplines. As previously discussed, and as popular culture has long dramatized, the construction industry operates on equally volatile terrain. It is a profession marked by fluctuating costs, unpredictable schedules, and ever shifting regulatory and market environments. Unfortunately, the adoption of MCS in AEC workflows has lagged far behind.

The Monte Carlo Method, of which “simulation” is a part of, resists a single definition, as its many variations all share a core process: modeling a system using probability density functions (PDFs), repeatedly sampling from these distributions, and compiling statistics to reveal patterns or risks. From modeling the arc of a thrown football to simulating photon paths in emission tomography, MCS scale from the simple to the staggeringly complex. Defining a model involves determining which outputs are most relevant, the required level of precision, how inputs are measured, and how the underlying processes are to be represented.  The required accuracy hinges on the question posed: a weather forecast for a picnic demands less precision than one for farming irrigation. Current computational limits force tradeoffs. Simulating every subatomic interaction is impossible, let alone the economy or subcontractor interactions on a job site, so models must rely on estimates and approximations.

At its core, each simulation draws from PDFs, mathematical descriptions of how likely different values are for a given input, such as work package lengths or material costs. The more accurately these distributions reflect reality, the more useful the model becomes: a classic case of the old “garbage in, garbage out” trope. Given that, MCS’ are only as “random” as we make them. The shape of each distribution, its average, spread, and tails, is chosen deliberately, based on past data, expert opinion, and/or institutional bias. A bell curve (normal or uniform distribution) assumes a most likely outcome flanked by rare extremes, while a triangular distribution might emphasize a tighter range of expected results. Each of these choices inherently bakes in some determinism into the model. This is a critical consideration for the AEC industry. Assuming too narrow a spread for labor productivity introduces delay risks; assuming too broad a range for material pricing introduces cost risks — both of which can kill a project (Smith, 2014). So even though Monte Carlo is a tool for navigating chance, the modeler’s hand still guides the wheel.

Literature Review & Case Study

While some studies champion Monte Carlo Simulation for its ability to generate risk informed forecasts of cost and time (Acebes et al., 2015 and Rezaee Arjroody et al., 2023), its application tends to cluster in specific domains: infrastructure megaprojects, defense contracting, or advanced project management contexts. Meanwhile, mainstream construction workflows and architectural processes largely continue to rely on deterministic models, i.e. Excel, leaving a methodological gap between the complexity of the built environment and the tools we use to design and build it. This review explores that gap by examining a few academic contributions.

Recent studies have expanded the scope of MCS by integrating it with other analytical methods, such as Bayesian networks, to model both the likelihood and interdependence of risks. Chen et al. (2020), for instance, developed a hybrid Bayesian MCS driven approach for construction schedule risk inference in complex infrastructure projects. Their method incorporates network theory to define risk correlations, constructs Bayesian structures algorithmically, and eliminates the need for observational data by using probabilistic inference. This approach allows for a more flexible and scalable risk modeling framework, particularly suited to data rich infrastructure environments. However, despite its theoretical strength, the study also highlights a broader industry challenge: even highly refined models face adoption barriers due to time, data, and expertise constraints, especially outside of infrastructure, in more variable or speculative forms of construction.

While much of the literature on MCS in construction remains abstract or overly focused on methodology, the study by Dikmen et al. (2019) stands out for integrating MCS into the logic of an actual highrise project. Their case study centers on a Class A office tower in Istanbul, using a Line-of-Balance schedule and simulating various crew performance scenarios over repeated work units. But unlike many studies where MCS is treated as an academic overlay, the simulation here functions as an active risk diagnostic, confronting the project team with the uncomfortable reality that the planned 292 day schedule only had about a 30% chance of being met. This prompted the project team to reconsider the robustness of their assumptions and explore targeted interventions, such as crew reallocation strategies and schedule buffers. The key lesson was not about identifying risk but about shifting the mindset around how risk is communicated, understood, and acted upon. The model’s ability to translate abstract variability into tangible outcomes proved essential for gaining buy-in across stakeholders.

This case is valuable not because the method itself was novel [it was not] but because it illustrates how MCS can be embedded into the workflow of real, messy, time  sensitive construction projects. Rather than using simulation to prove a point, the authors use it to raise questions: What assumptions are driving our schedule? What if they’re wrong? Where are we most vulnerable? This application highlights the disconnect between the potential of MCS and its actual use in the field. It suggests that the challenge is not one of capability, but of culture. Firms often default to deterministic tools not because they lack access to probabilistic methods, but because the organizational habits and incentives simply don’t reward that kind of foresight. The Dikmen case shows what it looks like when those assumptions are momentarily suspended, and when the model is allowed to speak plainly.

Beyond scheduling and cost estimation, Monte Carlo Simulation has found applications in manufacturing adjacent areas of construction, particularly in tolerance analysis for prefabricated assemblies. A recent study by Rausch et al. (2019) applied MCS to predict geometric variability in offsite construction, comparing probabilistic outcomes against both as-built deviations and traditional tolerance chain methods. The Monte Carlo method produced more accurate and defensible estimates than either the overly optimistic root-sum-square method or the conservative worst-case approach, and it enabled process optimization that reduced rework risk by 65.6%. This is a good but uncommon example of MCS being used in a high-variability AEC context and highlights the flexibility of MCS as a design aid. Yet even here, the goal of simulation is not to explore uncertainty per se, but to suppress it, to reduce geometric drift and tighten assembly tolerances.

To better understand how MCS is perceived and applied in academia, I conducted an interview with DR. Hyun Woo “Chris” Lee, a professor in the University of Washington’s Construction Management (CM) department whose research spans sustainability, finance, and probabilistic methods. With nearly two decades of experience using MCS, initially introduced during his graduate studies and regularly applied to research in energy retrofits, solar policy, and operations management, his perspective bridges academic expertise and pedagogical pragmatism.

When asked about the use of MCS in industry, his response was direct: “None. Nobody’s using it.” In his view, while the financial sector and even real estate to an extent embrace probabilistic modeling due to the clear value proposition tied to risk, construction remains rooted in deterministic logic. This is not for lack of interest, he explained, but a mix of cultural inertia, limited computational skillsets, and unclear payoff in practice. He emphasized that even in education, where there is more flexibility to introduce simulation based thinking, MCS proves challenging for students without strong quantitative backgrounds. Despite early efforts to teach MCS through Excel based assignments in CM courses, he eventually scaled back its use, finding that the majority of students struggled to implement the models effectively.

Its difficult for him to remain optimistic about the potential for MCS to be adopted more widely in its current state. In areas like construction operations management, where the logic of repeated tasks and variable durations is intuitive and lends itself well to simulation, he sees a bit more upside. He was more excited for AI tools as potential catalysts for change however, by lowering the coding barrier and automating parts of the modeling process, they might make stochastic thinking more accessible to practitioners who currently find it out of reach. This seems like it would be instrumental step forward in the education and communication aspects, and induce a democratization that other niche software’s like CAD and BIM have enjoyed. After all, MCS has not changed much since its early days. Dr. Lee noted that he routinely uses the same MATLAB models in his work that he used as a grad student decades ago.

“So there is supposed to be a need first. Like, they have to see a value of doing MCA first. I don’t think construction people are seeing that value yet. Do I expect that they will see the value in five years? I don’t think so. In 10 years? I don’t know.”

Most notably, he reinforced that MCS excels not by providing precise answers, but by helping researchers and planners wrestle with uncertainty in structured ways. “Complicated problems that have a lot of uncertainties can be best represented with MCS,” he explained. “That typically happens in research, not in the practice world. But it should.” This perspective not only reinforces the central argument of this paper, that MCS remains underutilized in construction despite its practical potential, but also highlights the conditions under which adoption may become more feasible.

Analysis

What emerges from the preceding literature, case study, and expert opinion is not merely a gap between theory and practice, but a failure of imagination around how probabilistic thinking might reshape construction workflows, roles, and even identity. Existing research often assumes that better tools or more training will lead to broader adoption of digital tools, MCS included. But perhaps that assumption misses something more fundamental.

One might expect that the construction industry, where projects are site specific, path dependent, and laden with ambiguity, would be natural adopters of probabilistic methods, yet, simulation finds more traction in sectors with stable inputs and repeatable processes (infrastructure, energy, defense). This inversion raises a deeper question: is MCS only being adopted where uncertainty is already minimized? If so, then MCS is being used to fine tune control, not to embrace or explore indeterminacy. That presents a challenge to the core narrative of simulation as a tool for navigating complexity. The literature rarely acknowledges this dynamic, and case studies like Dikmen et al. (2019) only hint at it.

Much of the existing research treats MCS as a neutral tool, but it is often the domain of technical experts, consultants, or academics. What is largely absent from both the literature and practice is a framework for democratized simulation. In the same way that BIM was eventually reframed as a collaborative, multi-authoring tool, MCS may need a similar cultural shift, away from single  user technical modeling and toward shared, iterative, low stakes forecasting. That could mean simulation embedded in design charrettes or early feasibility studies for example, not just post-design risk audits. Yet, no study found has leaned into the organizational logistics of a “shared simulation” and who builds it/owns it/trusts it. This absence may be less about technical limitations and more about an underexplored social dimension of modeling, where simulation is treated not only as analysis, but as a platform for dialogue. Whether this vision is practical or naive remains an open question, but it suggests a direction for future research that bridges the gap between tool and team. Then again, does your phone’s calculator really need an IoT integration?

The widespread underuse of simulation may reveal more about the structure of AEC practice than about the tool itself. MCS is not just underutilized, it is often intentionally avoided. Its outputs are uncertain, its inputs are arguable, and its conclusions are contingent. In an industry governed by deliverables, liability, and schedule based billing, these qualities are liabilities. Perhaps the industry’s resistance to MCS is not technical at all, but epistemological. Simulation exposes how little we know. It resists the closure that clients demand and reveals the fiction of predictability that so much of project management rests upon. In this light, MCS’s limited uptake is not a problem to be solved but a tension to be acknowledged.

This section does not resolve these questions, but raises them to complicate the dominant narrative that simulation is simply a good idea waiting for better implementation. If the goal is to expand the role of MCS in construction, it may be time to rethink not just the tools or training, but the underlying logics that shape how we model, predict, and plan.

Example

This mini case study would not be complete without an actual Monte Carlo Simulation to illustrate how probabilistic planning can be applied in the context of construction. The Dikmen et al. case sets the stage for a simplified schedule model. If that study represents what MCS looks like when fully integrated into a large, resource heavy project, then this example attempts the opposite: to show how probabilistic reasoning can be brought down to earth and applied in a pint sized spreadsheet based format. While basic in its setup, the example that follows shares the same goal of revealing the full shape of uncertainty and challenging the illusion that planning is ever a certainty. Similarly, in academia a more robust analysis would tackle this in a dedicated computation platform like Python or MATLAB, but in order to make a compelling value proposition, I will use Microsoft Excel, a program embedded into the daily workflows of architects, engineers,  and construction managers worldwide.

Creating this MCS model was far from a plug-and-play exercise. It took nearly two hours of trial, error, and tweaking to settle on the right balance of formulas and logic that realistically but simply represent construction delays. The process began by defining core parameters grounded in industry realities: a weekly 85% chance that work proceeds on schedule (5 day delay), a 10% chance that weather related delays intervene (2 day delay), and fixed durations for both routine and weather induced delays. Translating these probabilities into Excel formulas required careful layering of conditional logic combined with random number generation to somewhat mimic real world randomness. Initially, formulas returned zeros or inflated results, exposing the subtle pitfalls of referencing cells, mixing absolute and relative references, and managing how Excel interprets Boolean logic in arithmetic operations. Tweaking these issues demanded patience and attention to detail, because even a small slip in formula structure can distort the entire simulation. While this model is necessarily a simplification, abstracting from the full complexity of construction processes and interdependent risks, it nevertheless serves as an quick and easy demonstration for a project scheduling problem. The model can be expressed as a discrete-time stochastic process simulating delays over a 20 week construction schedule (5 day work weeks, 100 work days). Each week, two types of delay are independently assessed: supply chain delays and weather related interruptions.

 Let T = 20 represent the total number of construction weeks. For each week t ∈ {1, 2, …, T}, two independent probabilistic events may introduce delay: A supply chain delay occurs with probability (1 – p_d), contributing δ_d days of delay if triggered,  or a weather delay occurs with probability p_w, contributing δ_w days of delay if triggered.

The total delay in week t is given by:

Delay_t = Bernoulli(1 – p_d) × δ_d + Bernoulli(p_w) × δ_w

The cumulative project delay across the full construction period is:

Total Delay = Σ (from t = 1 to T) Delay_t

To model this in Excel, we begin by creating three sheets: “Parameters”, “Simulation”, and “Summary”. The Parameters sheet stores model inputs so they can be easily referenced and adjusted without rewriting entire formulas. The Simulation sheet then runs the math: each row represents one trial of a 20 week construction schedule, and each column corresponds to a week. Delay outcomes are calculated using a combination of RAND() functions and IF() statements, which mimic Bernoulli trials. For example, if the random number exceeds the probability of on-time supply delivery, the formula adds a fixed delay value. Similarly, a separate random draw determines whether weather causes further delay. These are summed across each week to produce a total delay figure per trial. The Summary sheet aggregates the simulation results into descriptive statistics: average and median project duration, minimum and maximum durations, standard deviation, and the percent of trials that finish on time (<105 days), allowing us to visualize not just the central tendency but the long tail of risk.

To build the simulation logic, begin in cell B2 of the Simulation sheet. Assume that A2 contains the simulation number (e.g., 1), and that Row 1 holds the column headers (Simulation Number, Week 1 through Week 20, Total Delay, Total Duration, and so on.), as well as Parameters being organized from cell B2 to B5, the equivalent weekly formula for a single week’s delay is written as:

=IF(RAND() > Parameters!$B$2, Parameters!$B$3, 0) + IF(RAND() < Parameters!$B$4, Parameters!$B$5, 0)

Where Parameters!$B$2 = pd = 0.85,  Parameters!$B$3 = δd = 5, Parameters!$B$4 = pw = 0.1, and Parameters!$B$5 = δw = 2. Each of the 20 weekly columns contains this formula, one per week. A final “Total Delay” column, cell V2, sums across all 20 weeks:

=SUM(B2:U2)

Once the logic was locked in, the model ran 10,000 simulations to capture a statistically meaningful spectrum of outcomes. In this case, “running the model” means copying cell A2 all the way to A10001. Each iteration generates a weekly delay scenario, summing delays to reveal the total project extension across the 20 week timeframe. The outputs are raw data arrays with total delay numbers. It may be worth taking the extra step in defining appropriate bins to smooth out spikes in the data before constructing a bar chart and cumulative distribution function (CDF) graph. These are the most common ways of visualizing and communicating MCS data.

The following results for this example construction delays scenario illustrate the average duration is approximately 119 days, far exceeding the planned 100 day schedule. The median duration closely matches this average, indicating a generally symmetric distribution, though outliers extend the maximum duration to 156 days. The minimum duration aligns with the baseline schedule at 100 days. A standard deviation of 8.53 days reflects moderate variability around the mean, while only about 4.77% of simulations complete on or before the target of 105 days, emphasizing the rarity of finishing truly on time under modeled uncertainties. The following graphs illustrate the MCS outputs visually. The resulting clustered bar graph reveals a relatively spiky distribution despite binning, with most projects clustering in the 110-130 day mark. A CDF (incorrectly titled “Cumulative Probability Function” below) further shows that only about 10% of the 10,000 simulations finish within a week of the original timeline, 50% finish within 3 weeks, and 90% finish within a month. The moral of this story given the inputs is to avoid construction kick-off during an ongoing trade war and/or fire season.

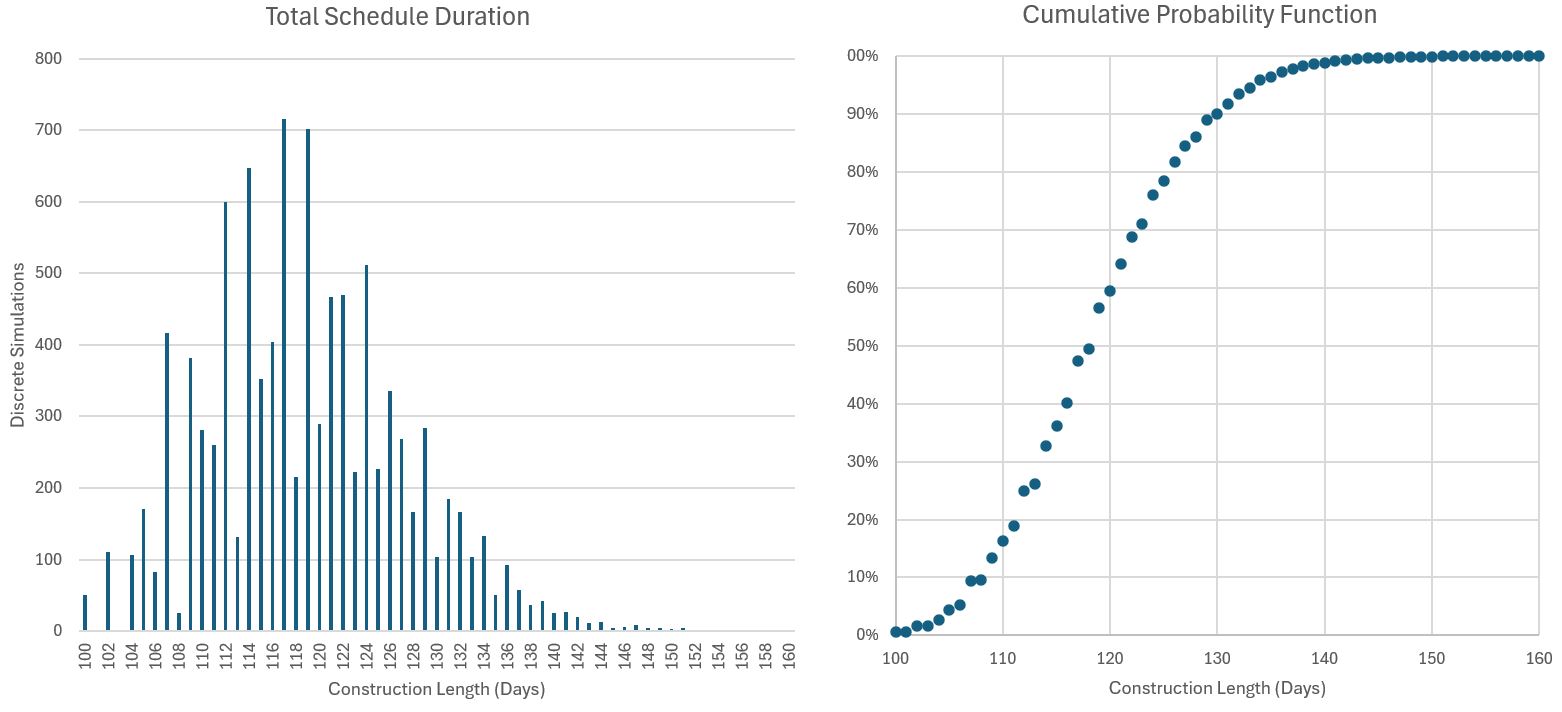
To test the model’s sensitivity, the simulation was re-run with more adverse input conditions: a 60% weekly on time delivery rate and a 25% chance of weather delay. The resulting output PDF distribution was much smoother and indicative of a normal distribution. Despite modest delay durations (2 days for supply, 1 for weather), the average project length rose to 121.05 days, with only 0.05% of simulations finishing within 105 days. These conditions also shift the 90% completion odds to the left to the 126th day as opposed to the 130th. Compared to the base scenario, this version illustrates how frequent, small disruptions can compound into systemic delay. 

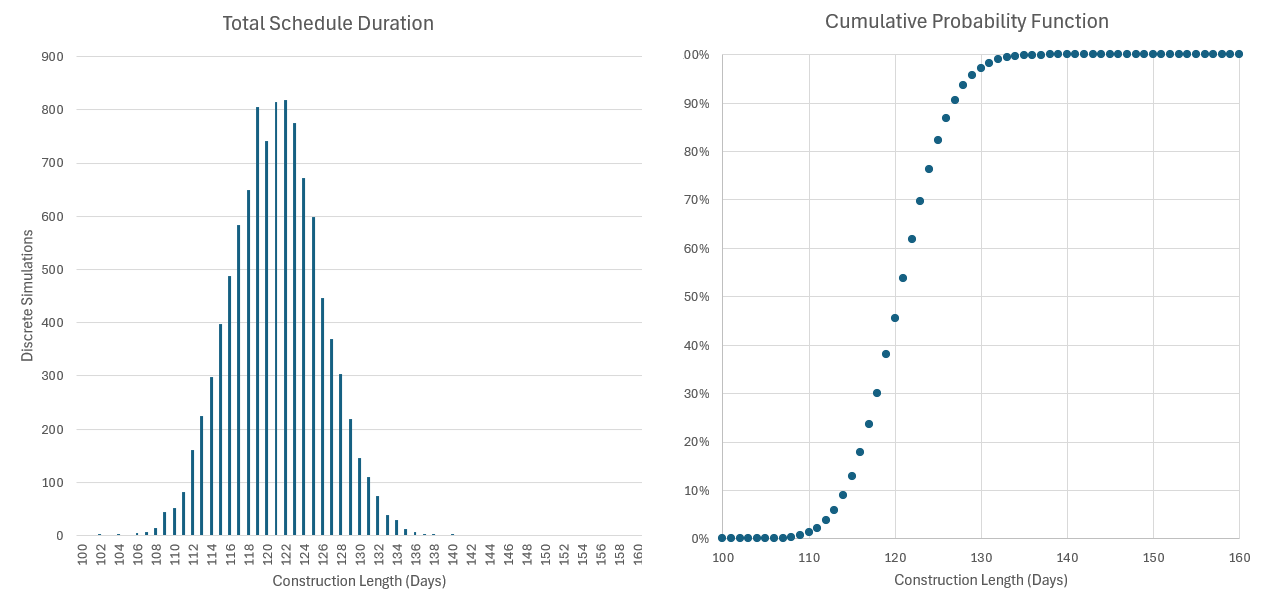
This model is deliberately simple, using fixed input values (e.g. 60% on-time delivery, 25% chance of weather delay) rather than probabilistic distributions. While this avoids the complexity of modeling full input ranges, it also limits the model’s fidelity. In real-world applications, uncertainties are often better represented by distributions (normal, triangular, beta, etc.) that capture second-order risk and allow for more nuanced sensitivity analyses. Revisiting the model to implement these was beyond the current scope, but the omission points to a clear opportunity for refinement.

With that being said, probability distributions as inputs can become a double edged sword for practitioners entrenched in fast paced, high stakes construction environments. First, defining accurate distributions demands historical/detailed/project specific data that many firms simply do not have or cannot reliably access. Without robust data, distributions can become guesswork, undermining the model’s credibility. Second, interpreting and communicating probabilistic outputs requires statistical literacy that is often missing in typical project teams. Decision makers comfortable in deterministic schedules may find probabilistic results abstract or overwhelming, impeding clear action. Third, building and running distribution based models in tools like Excel can be computationally heavier and more complex to set up, clashing with practitioners’ preference for straightforward, “black-and-white” answers. Lastly, organizations locked into traditional workflows and risk averse cultures may resist the added nuance, fearing it complicates rather than clarifies decisions. Together, these barriers mean that, while theoretically superior, probability distributions could remain aspirational rather than operational in the job site  trailer.

This somewhat painstaking, hands on experience highlights both the promise and the pragmatism of Monte Carlo Simulation in the AEC world. Setting up even a relatively simple model in Excel proved far more cumbersome than expected, and that is said by someone who has used more advanced MCS tools. Despite Excel’s ubiquity, its native limitations made the process feel surprisingly manual, error prone, and fragile. Each step required back and fourth and workarounds that, while conceptually straightforward, demanded an unappreciated amount of spreadsheet acrobatics. And this was for a toy model. A real world model would have a few more levels of depth to actually be useful.

This experience underscores the sentiment that the implementation of MCS is easier conceptualized than done. That disconnect helps explain why simulation remains underused in construction, as its tools do not meet practitioners where they are. Excel was chosen precisely because it reflects the software ecosystem familiar to most construction managers and architects, far from specialized environments like Python or MATLAB. But this choice revealed the deeper issue: the absence of user friendly, domain specific tools that integrate probabilistic thinking into real world workflows. MCS is no silver bullet, as it demands thoughtful input selection, validation, and interpretive nuance.

Discussion

Modeling in Excel remains one of the most accessible ways to understand the nuts and bolts of Monte Carlo Simulation. Its transparency and flexibility make it ideal for learning how assumptions, distributions, and iterations work together to produce probabilistic outputs. That said, every tool comes with a learning curve as demonstrated. The challenge, however, is not just technical, but cultural. How do we normalize simulation as part of the early design and planning process, rather than relegating it to post-hoc analysis, if anything at all? MCS integration tools for Excel exist (@Risk, Crystal Ball), but they’re niche, clunky, and relatively expensive (both in time and money). One practical step forward may be the creation of modular Excel templates with varying levels of depth tailored to different roles like construction managers, consulting engineers, architects, and even real estate developers. These templates would not eliminate the need for interpretation, but they could offer a more accessible entry point for teams to begin experimenting with uncertainty in a structured way. As with early adoption of BIM, familiarity may lead to fluency.

While the academic conversation around MCS in construction is quieter than in fields like finance or energy, it is far from silent, and it often speaks with a stronger accent abroad. Although I lack quantitative data to confirm it, a majority of the scholarly case studies and discourse I reviewed appears to originate from outside North America. It is unclear why this is the case, but the pattern is clear enough to invite attention. Whether due to educational emphasis, regulatory differences, or cultural attitudes toward risk, the relative silence in North American construction literature is notable. Similarly, the literature connecting MCS directly to construction was often scattered across niche or inconsistent journals. This fragmentation made it difficult to locate comprehensive or comparative studies. The lack of a consolidated body of work may itself be a barrier to broader adoption, and if practitioners and students cannot easily find examples, they are unlikely to replicate or build upon them.

Ultimately, the underuse of simulation in construction is telling of a potentially deeper tension. Probabilistic tools like MCS promise to help us navigate uncertainty, yet their uptake is most common in environments where uncertainty has already been disciplined and contained. Perhaps this is not a failure of implementation, but a reflection of deeper epistemological discomfort: simulation does not promise certainty, only insight. And in a profession that prizes deliverables, closure, and authority, such ambiguity can be difficult to accept. If the industry resists tools that expose how little is known, the challenge ahead is not just about modeling uncertainty, it is about confronting it.

Acknowledgements

The example Monte Carlo Simulation model was developed with assistance from OpenAI’s ChatGPT, which provided guidance on probabilistic modeling strategies, mathematical and Excel formula implementation, and refinement of explanatory text.

Special thanks to Dr. Lee for agreeing to the interview with me, and to Dr. Dossick, who enabled healthy discussion and provocative ideas during class time for the 2025 edition of the Innovation in Construction course.

References

Acebes, F., Pereda, M., Poza, D., Pajares, J., & Galán, J. M. (2015). Stochastic earned value analysis using Monte Carlo Simulation and Statistical Learning Techniques. International Journal of Project Management, 33(7), 1597–1609. https://doi.org/10.1016/j.ijproman.2015.06.012 

Chen, L., Lu, Q., Li, S., He, W., & Yang, J. (2021). Bayesian Monte Carlo Simulation–driven approach for construction schedule risk inference. Journal of Management in Engineering, 37(2). https://doi.org/10.1061/(asce)me.1943-5479.0000884

Kwak, Y. H., & Ingall, L. (2007). Exploring Monte Carlo simulation applications for project management. Risk Management, 9(1), 44–57. http://www.jstor.org/stable/4143844

Metropolis, N., & Ulam, S. (1949). The Monte Carlo method. Journal of the American Statistical Association, 44(247), 335-341. https://doi.org/10.1080/01621459.1949.10483310

Rausch, C., Nahangi, M., Haas, C., & Liang, W. (2019). Monte Carlo simulation for Tolerance Analysis in prefabrication and offsite construction. Automation in Construction, 103, 300–314. https://doi.org/10.1016/j.autcon.2019.03.026

Rezaee Arjroody, A., Hosseini, S. azim, Akhbari, M., Safa, E., & Asadpour, J. (2023). Accurate estimation of cost and time utilizing risk analysis and Simulation (CASE Study: Road Construction Projects in Iran). International Journal of Construction Management, 24(1), 19–30. https://doi.org/10.1080/15623599.2023.2210476

Smith, N. J. (2014). Managing risk in construction projects (pp. 77-78). John Wiley & Sons, Inc.

Tokdemir, O. B., Erol, H., & Dikmen, I. (2019). Delay risk assessment of repetitive construction projects using line-of-balance scheduling and Monte Carlo Simulation. Journal of Construction Engineering and Management, 145(2). https://doi.org/10.1061/(asce)co.1943-7862.0001595

Wang, X.-X., & Huang, J.-W. (2009). Risk analysis of construction schedule based on Monte Carlo simulation. In 2009 International Symposium on Computer Network and Multimedia Technology (pp. 1-4). IEEE. https://doi.org/10.1109/CNMT.2009.5374816

About the author

name: Nicholas Miranda

institution: University of Washington

Nicholas is an aspiring architect-developer and self-proclaimed “Ideas Guy” exploring how quantitative analysis can reshape how we design cities. Currently pursuing his Master of Architecture at the University of Washington-Seattle, his work bridges the gap between aesthetics, and economics, with a focus on high-rise housing and urban infill. A lifelong Floridian and veteran of the U.S. Air Force, Nicholas brings discipline, curiosity, and an entrepreneurial spirit to everything from his design studios to advocacy organizations. Beyond architecture, he’s an avid sailor, Latin dancer, and space exploration enthusiast.